范式

1. 第一范式（1NF）

符合1NF的关系（你可以理解为数据表。“关系模式”和“关系”的区别，类似于面向对象程序设计中”类“与”对象“的区别。”关系“是”关系模式“的一个实例，你可以把”关系”理解为一张带数据的表，而“关系模式”是这张数据表的表结构。1NF的定义为：符合1NF的关系中的每个属性都不可再分。表1所示的情况，就不符合1NF的要求。

2. 第二范式（2NF）

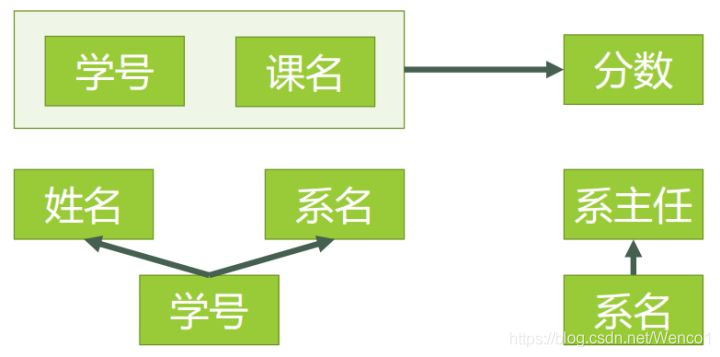
设 K 为某表中的一个属性或属性组，若除 K 之外的所有属性都完全函数依赖于 K（这个“完全”不要漏了），那么我们称 K 为候选码，简称为码。在实际中我们通常可以理解为：假如当 K 确定的情况下，该表除 K 之外的所有属性的值也就随之确定，那么 K 就是码。一张表中可以有超过一个码。（实际应用中为了方便，通常选择其中的一个码作为主码） 例如：对于表3，（学号、课名）这个属性组就是码。该表中有且仅有这一个码。（假设所有课没有重名的情况）

2.3 非主属性

包含在任何一个码中的属性成为主属性。

例如：
对于表3，主属性就有两个，学号 与 课名。

终于可以回过来看2NF了。首先，我们需要判断，表3是否符合2NF的要求？根据2NF的定义，判断的依据实际上就是看数据表中是否存在非主属性对于码的部分函数依赖。若存在，则数据表最高只符合1NF的要求，若不存在，则符合2NF的要求。判断的方法是：

第一步：找出数据表中所有的码。
第二步：根据第一步所得到的码，找出所有的主属性。
第三步：数据表中，除去所有的主属性，剩下的就都是非主属性了。
第四步：查看是否存在非主属性对码的部分函数依赖。

对于表3，根据前面所说的四步，我们可以这么做：

第一步：

1. 查看所有每一单个属性，当它的值确定了，是否剩下的所有属性值都能确定。
2. 查看所有包含有两个属性的属性组，当它的值确定了，是否剩下的所有属性值都能确定。
3. ……
4. 查看所有包含了六个属性，也就是所有属性的属性组，当它的值确定了，是否剩下的所有属性值都能确定。

看起来很麻烦是吧，但是这里有一个诀窍，就是假如A是码，那么所有包含了A的属性组，如（A，B）、（A，C）、（A，B，C）等等，都不是码了（因为作为码的要求里有一个“完全函数依赖”）。
图4表示了表中所有的函数依赖关系：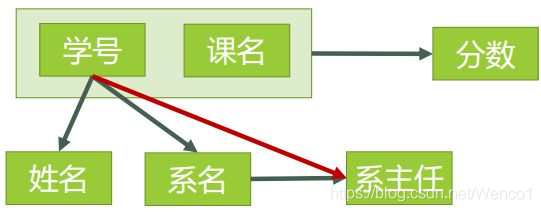

图4
这一步完成以后，可以得到，表3的码只有一个，就是 （学号、课名） 。

第二步：主属性有两个：学号 与 课名

第三步：非主属性有四个：姓名、系名、系主任、分数

第四步：
对于（学号，课名） → 姓名，有 学号 → 姓名，存在非主属性 姓名 对码（学号，课名）的部分函数依赖。
对于（学号，课名） → 系名，有 学号 → 系名，存在非主属性 系名 对码（学号，课名）的部分函数依赖。
对于（学号，课名） → 系主任，有 学号 → 系主任，存在非主属性 对码（学号，课名）的部分函数依赖。

所以表3存在非主属性对于码的部分函数依赖，最高只符合1NF的要求，不符合2NF的要求。

对于学生表，其码是学号，主属性是学号，非主属性是姓名、系名和系主任，因为码只有一个属性，所以不可能存在非主属性对于码 的部分函数依赖，所以此表符合2NF的要求。
图5表示了模式分解以后的新的函数依赖关系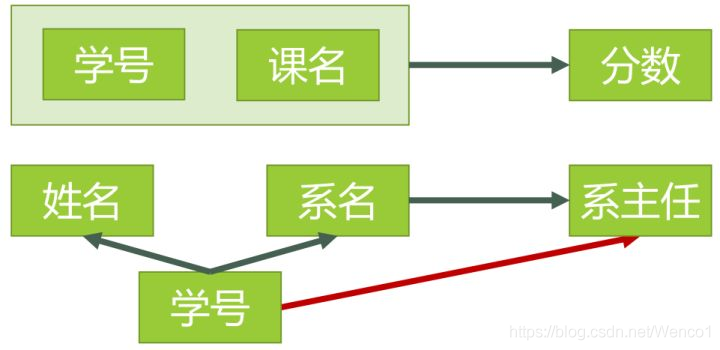

3. 第三范式（3NF）

3NF在2NF的基础之上，消除了非主属性对于码的传递函数依赖。也就是说， 如果存在非主属性对于码的传递函数依赖，则不符合3NF的要求。
接下来我们看看表4中的设计，是否符合3NF的要求。
对于选课表，主码为（学号，课名），主属性为学号和课名，非主属性只有一个，为分数，不可能存在传递函数依赖，所以选课表的设计，符合3NF的要求。
对于学生表，主码为学号，主属性为学号，非主属性为姓名、系名和系主任。因为 学号 → 系名，同时 系名 → 系主任，所以存在非主属性系主任对于码学号的传递函数依赖，所以学生表的设计，不符合3NF的要求。
为了让数据表设计达到3NF，我们必须进一步进行模式分解为以下形式：
选课（学号，课名，分数）
学生（学号，姓名，系名）
系（系名，系主任）
对于选课表，符合3NF的要求，之前已经分析过了。
对于学生表，码为学号，主属性为学号，非主属性为系名，不可能存在非主属性对于码的传递函数依赖，所以符合3NF的要求。
对于系表，码为系名，主属性为系名，非主属性为系主任，不可能存在非主属性对于码的传递函数依赖（至少要有三个属性才可能存在传递函数依赖关系），所以符合3NF的要求。。
新的函数依赖关系如图6