作业6

这一次作业比较简单，我们主要是需要对新的框架调整我们对应代码的格式。

//Render()
framebuffer[m++] = scene.castRay(ray,0); // castRay(ray, current_depth);

inline Intersection Triangle::getIntersection(Ray ray)
{
    Intersection inter;

    if (dotProduct(ray.direction, normal) > 0)  //判断是否能打在正面
        return inter;
    double u, v, t_tmp = 0;
    Vector3f pvec = crossProduct(ray.direction, e2);
    double det = dotProduct(e1, pvec); //Moller trumbore算法中分母接近于0 即入射光线和平面平行
    if (fabs(det) < EPSILON)
        return inter;
//......
}
Intersection(){
        happened=false;  //是否碰撞
        coords=Vector3f(); //碰撞坐标
        normal=Vector3f(); //平面法向
        distance= std::numeric_limits<double>::max(); //射线长度/距离(t)
        obj =nullptr; //相交的物体，对于这个三角形，其继承于object类，因此即为this
        m=nullptr; //material 
    }

Bounds3类中，存储了左下角及右上角两个点对来表示bounding box的边界。

附加部分实现SAH部分：

这一部分参考了：

https://zhuanlan.zhihu.com/p/50720158

https://blog.csdn.net/Q_pril/article/details/124054123

https://zhuanlan.zhihu.com/p/605710928

原slide：http://15462.courses.cs.cmu.edu/fall2015/lecture/acceleration/slide_026

[还有一篇参考？]

第一篇知乎专栏里介绍的比较清楚，其思想比较简单。

我们需要注意的是，在这里SAH作为一种启发式算法，只是选取了当前局部最优的情况，其贪心步骤仅考虑了当前情况的最优性，因此我们对每个object直接取了在当前节点进行相交的开销。

具体的，我们考虑一个根节点N，假设将其划分为两个子节点A和B，我们考虑两个开销，即和object直接判断相交的开销t，和遍历当前节点的开销$t{trav}$，我们假设无论是什么形状，其判断相交开销为1，$t{trav}$有经验值0.125。

最后我们有两个假设：

1.光线是完全随机分布的

2.光线不会和其他物体发生碰撞

此时我们有概率上的一个假设，即对于在凸包N中的凸包A，一条光线打到B的情况下，其同时打到A的概率为$P(hitA|hitN) = \frac{S(A)}{S(N)}$，其中S为该包围盒的表面积，设打到A的概率为P(A)，打到B的概率为P(B)，由于采用启发式算法，我们采用一个估值函数:

$c(A,B) = t_{trav} + P(A) N_A + P(B) N_B$

采用这个方法我们即考虑了空间中包围体的分布，也考虑了当前的块内所含的object数，可以达到较好的效果。

在实践中，我们可以选择对每个物体的最左端和最右端构建划分，并计算上面的值，当然这种方法的速度是较慢的。

我们可以采用桶的方式，对整个图形进行等距划分。

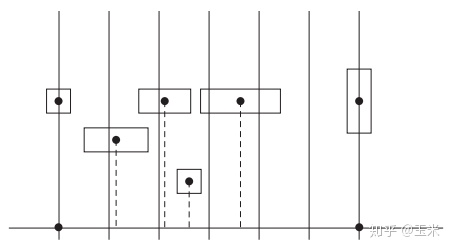
我们有具体算法如下，实践中，我们采用bucket_size < 32为佳：

这一部分的算法理论上来说实现是较为简单的，在实现过程中，我们考虑某个图元，其质心位置为t，则其属于第$B = Clamp(\frac{(t - t{min})}{t{max}-t_{min}}*n,0,n-1)$，我们需要这个clamp，主要是因为浮点数精度的问题，在后续我们也确实遇到了浮点数精度的问题。

我们对思路进行优化，即排序后我们正向和反向遍历整个列表，并计算第1~i个桶中所有物体的表面积、个数（反向则是最后一个到第i个），由于父亲节点的包围盒大小并不变，遍历复杂度为常数，我们仅需考虑表面积*个数的值即可。

计算完之后我们仅需遍历以i为分界的左边的桶和右边的桶的值的和取最小值即可。

其代码具体如下：

template<class T>
void BVHAccel::getBucketCost(std::vector<float> &bucket_cost, std::vector<int> &bucket_last_obj, T begin, T end,
                             const int &axis, const float &minn, const float &maxx) {

    auto getBucket = [minn,maxx](float a) {
        return  std::clamp((int)((a - minn) / (maxx - minn) * (bucket_size)),0,bucket_size-1);
    };
    Bounds3 bound;
    int cur_bucket = 0;
    for(auto i = begin; i < end; i++){
        int bucket_i;
        switch(axis){
            case 0:
                bucket_i = getBucket((*i)->getBounds().Centroid().x);
                break;
            case 1:
                bucket_i = getBucket((*i)->getBounds().Centroid().y);
                break;
            case 2:
                bucket_i = getBucket((*i)->getBounds().Centroid().z);
                break;
        }

        if(bucket_i != cur_bucket){
            for(int x = cur_bucket; x < bucket_i; x++){
                bucket_last_obj[x] = i - begin;
                bucket_cost[x] = bound.SurfaceArea();
            }
            cur_bucket = bucket_i;
        }
        bound = Union(bound,(*i)->getBounds());
    }
}
BVHBuildNode* BVHAccel::recursiveBuildSAH(std::vector<Object*> objects)
{
    BVHBuildNode* node = new BVHBuildNode();

    // Compute bounds of all primitives in BVH node
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    if (objects.size() == 1) {
        // Create leaf _BVHBuildNode_
        node->bounds = objects[0]->getBounds();
        node->object = objects[0];
        node->left = nullptr;
        node->right = nullptr;
        return node;
    }
    else if (objects.size() == 2) {
        node->left = recursiveBuildSAH(std::vector{objects[0]});
        node->right = recursiveBuildSAH(std::vector{objects[1]});

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        Bounds3 centroidBounds;
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
                    Union(centroidBounds, objects[i]->getBounds().Centroid());
        float best_cost = kInfinity;
        std::vector<Object*> leftshapes,rightshapes;
        for(int i=0; i<3; i++){
            std::vector<float> bucket_cost_l(bucket_size);
            std::vector<float> bucket_cost_r(bucket_size);
            std::vector<int> bucket_last_obj_l(bucket_size);
            std::vector<int> bucket_last_obj_r(bucket_size);
            float minn,maxx;
            switch (i) {
                case 0:
                    std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                        return f1->getBounds().Centroid().x <
                               f2->getBounds().Centroid().x;
                    });
                    minn = centroidBounds.pMin.x;
                    maxx = centroidBounds.pMax.x;
                    break;
                case 1:
                    std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                        return f1->getBounds().Centroid().y <
                               f2->getBounds().Centroid().y;
                    });
                    minn = centroidBounds.pMin.y;
                    maxx = centroidBounds.pMax.y;
                    break;
                case 2:
                    std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                        return f1->getBounds().Centroid().z <
                               f2->getBounds().Centroid().z;
                    });
                    minn = centroidBounds.pMin.z;
                    maxx = centroidBounds.pMax.z;
                    break;
            }

//            std::sort(objects.begin(), objects.end(), [i](auto f1, auto f2) {
//                return f1->getBounds().Centroid()[i] <
//                       f2->getBounds().Centroid()[i];
//            });
            getBucketCost(bucket_cost_r, bucket_last_obj_r, objects.rbegin(), objects.rend(), i, maxx, minn);
            getBucketCost(bucket_cost_l, bucket_last_obj_l, objects.begin(), objects.end(), i, minn, maxx);
            float min_cost = kInfinity;
            int best_div = 0;
            for(int l=0;l<bucket_size - 1;l++){
                int r = bucket_size - (l + 2);
                float cost = bucket_cost_l[l] * bucket_last_obj_l[l] + bucket_cost_r[r] * (objects.size() - bucket_last_obj_l[l]);
                // a float accuracy error will occur here, seems have little affect on whole algorithm;
                // assert(bucket_last_obj_l[l] + bucket_last_obj_r[r] == objects.size());
                if(cost < min_cost){
                    min_cost = cost;
                    best_div = bucket_last_obj_l[l];
                }
            }
            if(min_cost < best_cost){
                leftshapes = std::vector<Object*>(objects.begin(),objects.begin() + best_div);
                rightshapes = std::vector<Object*>(objects.begin() + best_div,objects.end());
                //forget this sentence! fuck!
                best_cost = min_cost;
            }
        }
        //std::cout<<"Current objects.size() = "<<objects.size()<<std::endl;

        assert(objects.size() == (leftshapes.size() + rightshapes.size()));

        assert(leftshapes.size() != 0);
        assert(rightshapes.size() != 0);

        node->left = recursiveBuildSAH(leftshapes);
        node->right = recursiveBuildSAH(rightshapes);

        node->bounds = Union(node->left->bounds, node->right->bounds);
    }

    return node;
}

首先我们需要注意，尽管代码在类Vector3f中实现了对操作符[]的重载，但是我们在这里使用这个操作符会出现连接错误，代码中采用了switch-case的方法对轴进行枚举，这里的报错原因还不是很清楚。

其次我们需要注意代码中的bucket_last_obj_l、bucket_last_obj_r，这两个分别指明了从头开始及从尾开始遍历时第i个桶的下一个obj的下表，我们可以看到注释下的assert有时是不成立的，这就是浮点数精度的问题导致的，他会使我们的cost值出现一定的不正确，但对我们整个算法的性能影响不大。

最后是getBucketCost函数，在这个函数中，我们使用了模板对正向迭代器和逆向迭代器进行代表，我认为这种方法有一定的危险性，C++可能会提供更specified的方法。